メネラウスの定理の証明

f:id:manabilife:20210808191817p:plain

中学生でもメネラウスの定理を使って線分比を出す生徒がいますが、証明の確認がおろそかになりがち。メネラウスの定理の証明の手順がわかっていれば、メネラウスの定理を使うよりも速く解ける問題も多いですね。

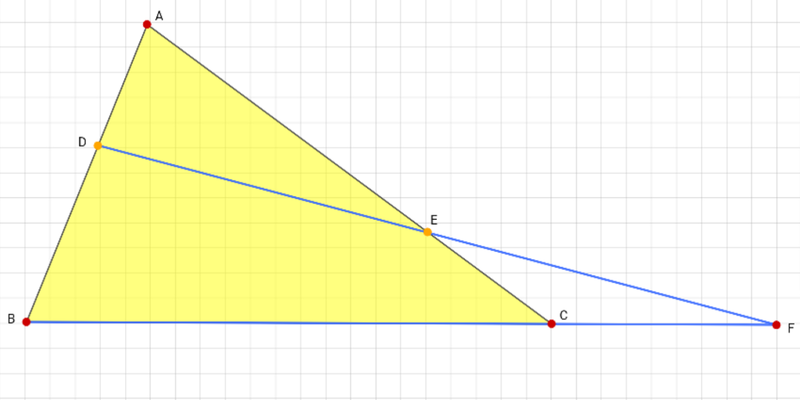
f:id:manabilife:20210808180158p:plain

図の三角形で、メネラウスの定理を使うと、

$\dfrac{DB}{AD}\times \dfrac{FC}{BF}\times \dfrac{EA}{CE}=1$

下図で三角形の交点（赤丸）、分点（青丸）の順に辿っていくのがポイントですね。

メネラウスの定理の証明では、下図のように点Cから辺FDに平行な線、辺CGを引きます。

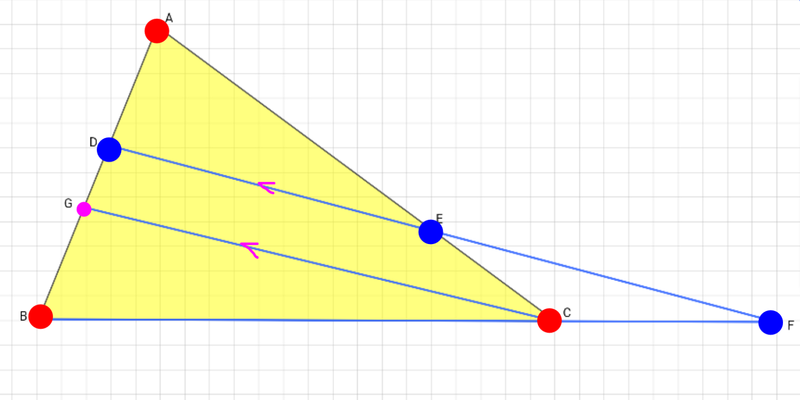
f:id:manabilife:20210808181148p:plain

$BG:GD:BD=BC:CF:BF$ より

$AD=BF\times \dfrac{AD}{BD}$

よって、

　 $AE:EC$

$=AD:DG$

$=BF\times \dfrac{AD}{BD}:CF$

メネラウスの定理の左辺に

$AE=BF\times \dfrac{AD}{BD}$

$EC=CF$

を代入すると

　 $\dfrac{DB}{AD}\times \dfrac{FC}{BF}\times \dfrac{BF\times \dfrac{AD}{BD}}{CF}$

$=\dfrac{DB}{AD}\times \dfrac{FC}{BF}\times \dfrac{BF\times AD}{BD\times CF}$

となり、全て約分できて１になりますね。

この証明の手順を把握していれば、メネラウスの定理を使わなくても、ブーメランの形があれば、条件と求めたい比に関係ない線に対して平行線を引けば、求めたい比を出すことができます。